Frequency Modulation, FM Sidebands & Bandwidth
The bandwidth of a frequency modulated, FM signal depends on a variety of factors including the level and frequency of the modulation, and their levels are important for broadcast and radio communication applications.
Frequency Modulation Tutorial Includes:
Frequency modulation, FM
Modulation index & deviation ratio
FM sidebands, bandwidth
FM demodulation
FM slope detector
FM ratio detector
Foster Seeley detector
PLL FM demodulator
Quadrature demodulator
MSK
GMSK
Modulation formats:
Modulation types & techniques
Amplitude modulation
Phase modulation
Quadrature amplitude modulation
The bandwidth, sideband formation and spectrum of a frequency modulated signal are not as straightforward as they are for an amplitude modulated signal.
Nevertheless the sidebands and bandwidth of the FM signal are still very important and used within the planning, design and even the maintenance of radio broadcast and radio communication systems.
Using a well know rule called Carson's Rule it is possible to provide a good estimate of the bandwidth of an FM signal. This estimate is sufficiently good for virtually all requirements and as a result Carson's rule is widely used.
Knowing the levels of the sidebands and the signal bandwidth is very important for broadcast transmitters and receivers as well as those sued for radio communication applications.
Frequency modulation sidebands
The modulation of any carrier in any way produces sidebands. For amplitude modulated signals, the way in which these sidebands are created and their bandwidth and amplitude are quite straightforward. The situation for frequency modulated signals is rather different.
The FM sidebands are dependent on both the level of deviation and the frequency of the modulation. In fact the total spectrum for a frequency modulated signal consists of the carrier plus an infinite number of sidebands spreading out on either side of the carrier at integral multiples of the modulating frequency.
From the diagram it can be seen that the values for the levels of the sidebands rise and fall with varying values of deviation and modulating frequency.

It may also be helpful to have some tabulated values - from this it can be seen that for a modulation index of 2.41, the carrier falls to zero, and all the power is contained within the sidebands.
It can also be seen that for low levels of modulation index, the only sidebands that have any significant levels of power within them are the first, and possibly the second sidebands.
| Relative amplitudes of FM Sidebands for Different Modulation Indices |
||||||
|---|---|---|---|---|---|---|
| Relative sideband amplitude | ||||||
| Mod Index |
0 | 1 | 2 | 3 | 4 | 5 |
| 0.00 | 1.00 | |||||
| 0.25 | 0.98 | 0.12 | ||||
| 0.5 | 0.94 | 0.24 | 0.03 | |||
| 1.0 | 0.77 | 0.44 | 0.11 | 0.02 | ||
| 2.0 | 0.22 | 0.58 | 0.35 | 0.13 | 0.03 | |
| 2.41 | 0.00 | 0.52 | 0.43 | 0.20 | 0.06 | 0.02 |
In theory the sidebands of a frequency modulated signal extent out for ever. Fortunately outside the main signal area itself, the level of the sidebands falls away and for practical systems filtering all but removes them without any main detriment to the signal.
For small values of modulation index, when using narrow-band FM, NBFM, radio communication systems, the signal consists of the carrier and the two sidebands spaced at the modulation frequency either side of the carrier. The sidebands further out are minimal and can be ignored. On a spectrum analyzer the signal looks very much like the spectrum of an AM signal. The difference is that the lower sideband is out of phase by 180°.
As the level of the modulation index is increased other sidebands at twice the modulation frequency start to appear. Further increases in modulation index result in the level of other sidebands increasing in level.
Carson's Rule for FM bandwidth
The bandwidth of an FM signal is not as straightforward to calculate as that of an AM signal.
A very useful rule of thumb used by many engineers to determine the bandwidth of an FM signal for radio broadcast and radio communications systems is known as Carson's Rule. This rule states that 98% of the signal power is contained within a bandwidth equal to the deviation frequency, plus the modulation frequency doubled. Carson's Rule can be expressed simply as a formula:
Where:
Δf = deviation
BT = total bandwidth (for 98% power)
fm = modulating frequency
To take the example of a typical broadcast FM signal that has a deviation of ±75kHz and a maximum modulation frequency of 15 kHz, the bandwidth of 98% of the power approximates to 2 (75 + 15) = 180kHz. To provide conveniently spaced channels 200 kHz is allowed for each station.
The rule is also very useful when determining the bandwidth of many two way radio communications systems. These use narrow band FM, and it is particularly important that the sidebands do not cause interference to adjacent channels that may be occupied by other users.
Equations & calculation for FM sideband levels
Whilst it is very useful to have an understanding of the broad principles of the generation of sidebands within an FM signal, it is sometimes necessary to determine the levels mathematically.
The calculations are not nearly as simple as they are for amplitude modulated signals and they involve some long equations. It is for this reason that rules like Carson's rule are so useful as they provide workable approximations that are simple and straightforward to calculate, whist being sufficiently accurate for most radio communications applications.
The sideband levels can be calculated for a carrier modulated by a single sine wave using Bessel functions of the first kind as a function of modulation index.
The basic Bessel function equation is described below:
Where:
α is an arbitrary complex number
In terms of the format of the equation, α and -α produce the same differential equation, but it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of α.
Solving the Bessel equations to determine the levels of the individual sidebands can be quite complicated, but is ideal for solution using a computer.
By manipulating the mathematics, it is possible to solve the basic Bessel function equation and express it in the format:
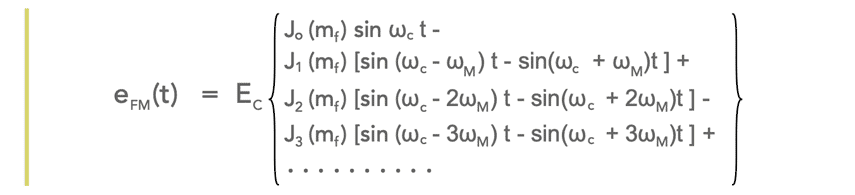
The way the series has expanded shows how the various sidebands are generated and how they extend out to infinity.
Summary of frequency modulation bandwidth & sidebands
Frequency modulation is still in widespread use, both for broadcasting and for two way radio communications. As a result, a knowledge of the signal bandwidth and the way in which the sidebands are produced is useful for these systems.
It is worth summarising some of the highlight points about frequency modulation sidebands, FM spectrum & bandwidth.
- The bandwidth of a frequency modulated signal varies with both deviation and modulating frequency.
- Increasing modulating frequency increases the frequency separation between sidebands.
- Increasing modulating frequency for a given level of deviation reduces modulation index. As a result, it reduces the number of sidebands with significant amplitude. This has the result of reducing the bandwidth.
- The frequency modulation bandwidth increases with modulation frequency but it is not directly proportional to it.
Frequency modulation bandwidth is a key issue as it is very important to ensure that these transmissions stay within their allocated channel. Accordingly FM signals need to be carefully tailored to ensure all the significant sidebands remain within the channel allocation.
More Essential Radio Topics:
Radio Signals
Modulation types & techniques
Amplitude modulation
Frequency modulation
OFDM
RF mixing
Phase locked loops
Frequency synthesizers
Passive intermodulation
RF attenuators
RF filters
RF circulator
Radio receiver types
Superhet radio
Receiver selectivity
Receiver sensitivity
Receiver strong signal handling
Receiver dynamic range
Return to Radio topics menu . . .