Quality Factor / Q Factor; formulas and equations
The quality factor or Q factor is a measure of the performance of a coil, capacitor inductor in terms of its losses and resonator bandwidth. Simple formulas can relate the variables.
Q, Quality Factor Tutorial Includes:
Q, quality factor basics
Inductor Q
RLC network Q
The quality factor or 'Q' of an inductor or tuned circuit is often used to give an indication of its performance in a resonator circuit and it is widely used in RF design and many other areas of electronic circuit design.
The Q or quality factor is a dimensionless number and it describes the damping in the circuit. It also provides an indication of the resonator’s bandwidth relative to its centre frequency.
Values for quality factor are often seen quoted and can be used in defining the performance of an inductor, a capacitor or a tuned circuit.
The Q or quality factor is used with many RF tuned circuits or elements to indicate their performance in an oscillator or other form of resonant circuit.
There are several simple formulas that relate the losses and bandwidth to the Q and these can easily be used to determine various aspects of a relevant circuit.
How the quality factor came about
The concept of Q, Quality Factor was first envisaged by an engineer named K. S. Johnson from the Engineering Department of the Western Electric Company in the US.
Johnson was evaluating the performance and quality of different coils. Over the course of his investigations he developed the concept of Q.
Interestingly his choice of the letter Q was made because all other letters of the alphabet were taken and not because of the term quality factor, although with hindsight the choice of the letter Q for quality factor could not have been any better.
Q factor basics
Quality factor is a concept that is applicable in many areas of physics and engineering. It is denoted by the letter Q and may be referred to as the Q factor.
The Q factor is a dimensionless parameter that indicates the energy losses within a resonant element which could be anything from a mechanical pendulum, an element in a mechanical structure, or within electronic circuit such as a resonant circuit.
While the Q factor of an element relates to the losses, this links directly in to the bandwidth of a resonator with respect to its centre frequency.
The Q indicates energy loss relative to the amount of energy stored within the system. Thus the higher the Q the lower the rate of energy loss and hence oscillations will reduce more slowly, i.e. they will have a low level of damping and they will ring for longer.
For electronic circuits, energy losses within the circuit are caused by resistance. Although this can occur anywhere within the circuit, the main cause of resistance occurs within the inductor.
Quality factor definition
The definition of quality factor is often needed to give a more exact understanding of what this quantity actually is. It is often helpful to have a concise form of words that explain what it is.
Quality Factor, Q definition:
For electronic circuits, Q is defined as the ratio of the energy stored in the resonator to the energy supplied by a to it, per cycle, to keep signal amplitude constant, at a frequency where the stored energy is constant with time.
From this it can be seen that the energy stored and lost are basically behind what the Q or a circuit is.
Q can also be defined for an inductor where it is the ratio of its inductive reactance to its resistance at a particular frequency, and it is a measure of its efficiency.
Similarly Q is also often used with capacitors and it is also important for varactor diodes where the losses in the diode can have a major impact upon the performance of any voltage controlled resonant circuit using the diodes.
Effects of Q factor
When dealing with RF tuned circuits, there are many reasons why Q factor is important. Usually a high level of Q is beneficial, but in some applications a defined level of Q may be what is required.
Some of the considerations associated with Q in RF tuned circuits are summarised below:
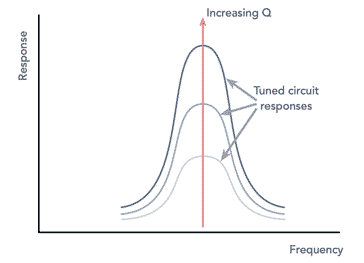
Bandwidth: With increasing Q factor or quality factor, so the bandwidth of the tuned circuit filter is reduced. As losses decrease so the tuned circuit becomes sharper as energy is stored better in the circuit.
It can be seen that as the Q increases, so the 3 dB bandwidth decreases and the overall response of the tuned circuit increases. In many instances a high Q factor is needed to ensure that the required degree of selectivity is achieved.
Wide bandwidth: In many RF applications there is a requirement for wide bandwidth operation. Some forms of modulation require a wide bandwidth, and other applications require fixed filters to provide wide band coverage.
While high rejection of unwanted signals may be required, there is a competing requirement for wide bandwidths. Accordingly in many applications the level of Q required needs to be determined to provide the overall performance that is needed meeting requirements for wide bandwidth and adequate rejection of unwanted signals.
Oscillator phase noise: Any oscillator generates what is known as phase noise. This comprises random shifts in the phase of the signal. This manifests itself as noise that spreads out from the main carrier.
As might be expected, this noise is not wanted and therefore needs to be minimised. The oscillator design can be tailored to reduce this in a number of ways, the chief one being by increasing the Q, quality factor of the oscillator tuned circuit.
- General spurious signals: Tuned circuits and filters are often used to remove spurious signals. The sharper the filter and the higher the level of Q, the better the circuit will be able to remove the spurious signals.
Ringing: As the Q of a resonant circuit increases so the losses decrease. This means that any oscillation set up within the circuit will take longer to die away. In other words the circuit will tend to "ring" more.
This is actually ideal for use within an oscillator circuit because it is easier to set up and maintain an oscillation as less energy is lost in the tuned circuit.
Q factor formulas
The basic Q or quality factor formula is based upon the energy losses within the inductor, circuit or other form of component.
From the definition of quality factor given above, the Q factor can be mathematically expressed in the Q factor formula below:
Where:
Q = quality factor of the circuit
Estored = energy that is stored
ELost per cycle = energy that is lost over each cycle
When looking at the bandwidth of an RF resonant circuit this translates to the Q factor formula:
Where:
Q = quality factor of the circuit
F0 = centre frequency of the tuned circuit
F-3dB is the frequency offset from the centre frequency where the response falls by 3 dB.

Within any RF or other circuit, each individual component can contribute to the Q or quality factor of the circuit network as a whole. The Q of the components such as inductors and capacitors are often quoted as having a certain Q factor or quality factor.
Quality factor and damping
One aspect of the Q factor that is of importance in many circuits is the damping. The Quality Factor, Q determines the qualitative behaviour of simple damped oscillators and affects other circuits such as the response within filters, etc.
There are three main regimes which can be considered when referring to the damping and Q factor.
Under-damped (Q > 1/2) : An under-damped system is one where the Q factor is greater than a half. Those systems where the Q factor is only just over a half may oscillate once or twice when a step impulse is applied before the oscillation falls away. As the quality factor increases, so the damping falls and oscillations will be sustained for longer.
In a theoretical system where the Q factor is infinite, the oscillation would be maintained indefinitely without the need for adding any further stimulus. In oscillators some signal is fed back to provide an additional stimulus, but a high Q factor normally produces a much cleaner result. Lower levels of phase noise are present on the signal.
Over-damped (Q < 1/2): An over-damped system has a Q factor that is less than 1/2. In this type of system, the losses are high and the system has no overshoot. Instead the system will exponential decay, approaching the steady state value asymptotically after a step impulse is applied.
As the Q factor or quality factor is reduced, so the systems responds more slowly to a step impulse.
Critically damped (Q = 1/2) : The critically damped system has a Q factor of 0.5 and like an over-damped system, the output does not oscillate, and does not overshoot its steady-state output. The system will approach the steady-state asymptote in the fastest time without any overshoot.
In many RF resonant systems, high levels of Q factor are needed. For filters sufficient selectivity is needed, but not too much, and for oscillators high levels of Q result in improved stability and lower phase noise. In many systems the Q factor should not be too high as it may result in filter bandwidths being too narrow and oscillators not being able to track over the required range. However Q factor levels need tend to be high rather than low.
The Q or quality factor is a key aspect of resonant and filter circuits, and especially within RF design. Q can also be important in other areas including general electronic circuit design as well as some aspects of audio design including loudspeakers and the like.
Having a basic understanding of Q will help provide a better understanding of some of the elements of circuit design and operation in a variety of areas.
More Basic Electronics Concepts & Tutorials:
Voltage
Current
Power
Resistance
Capacitance
Inductance
Transformers
Decibel, dB
Kirchoff's Laws
Q, quality factor
RF noise
Waveforms
Return to Basic Electronics Concepts menu . . .